Consider the following problem:

\begin{equation}
\begin{aligned}
P:= \min_{x_1,x_2} & f(x_1,x_2) \\\text{s.t. } x_1x_2 &\leq 1,\\ -10x_1-x_2 &\leq -6,\\ x_1 &\in [0,1.5],\\ x_2 &\in [1,4].
\end{aligned}
\end{equation}

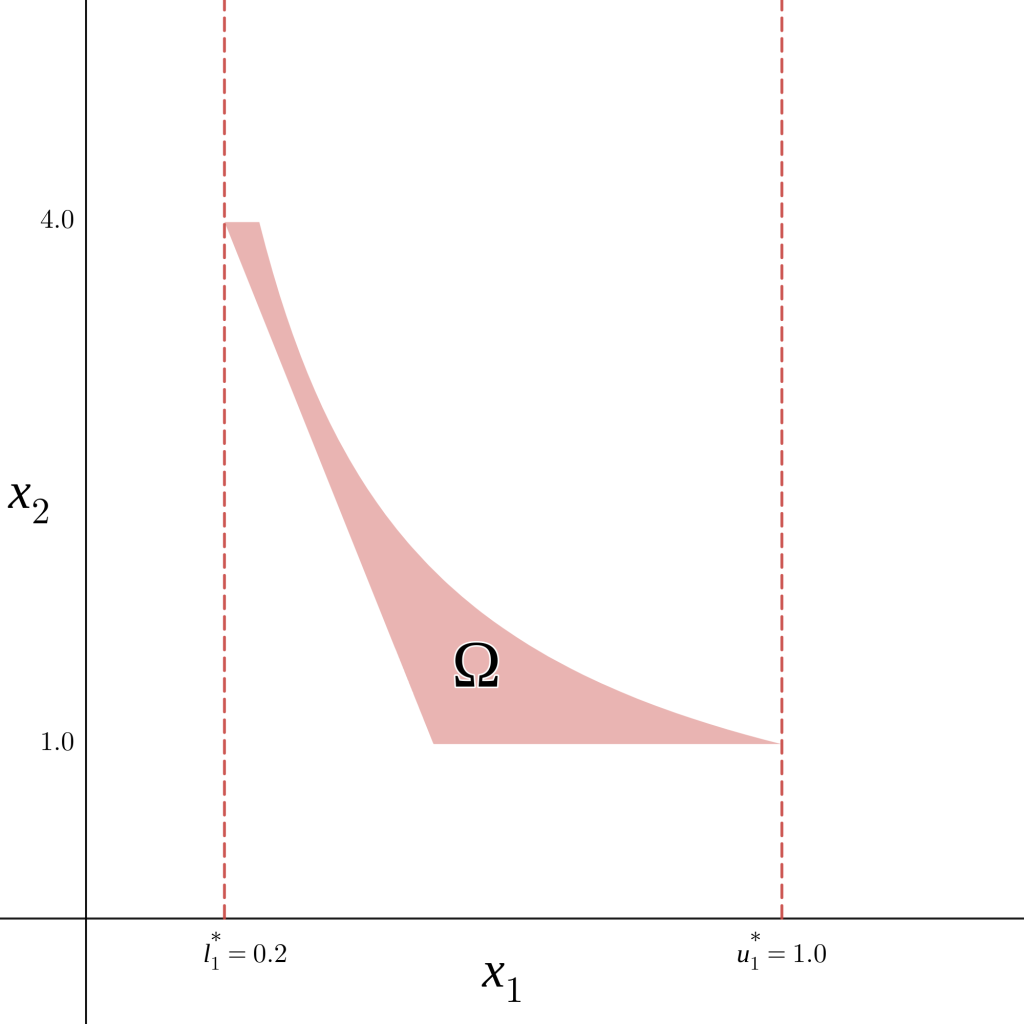
The feasible region for this problem corresponds to the red area in Figure 1, denoted as \(\Omega\).

Notice that although the range of the variable \(x_1\) is originally \([0,1.5]\), the feasible region in the figure only admits values of \(x_1\) between \(0.2\) and \(1\) (red dashed lines in Figure 1). Knowing this, it is then logical to change the bounds of \(x\) in the original problem from \(x_1 \in [0,1.5]\) to \(x_1 \in [0.2,1]\) (i.e., tightening the bounds of \(x_1\)).

This change will make other calculations and techniques used by Octeract Engine more effective (e.g., relaxations and branching).

In general, for a problem \(\min_{x \in \Omega} f(x)\) we would like to find the tightest bounds for each variable \(x_i\), i.e., find the lower bound \(l_i^\star = \min_{x \in \Omega} x_i\), and upper bound \(u_i^\star = \max_{x \in \Omega} x_i\).

However, unlike our previous example, it is not easy to solve the problems \(\min_{x \in \Omega} x_i\) and \(\max_{x \in \Omega} x_i\), and a different approach is required. Feasibility based bounds tightening (FBBT) , Optimisation based bounds tightening (OBBT) and Constraint propagation (CP), are some of the algorithmic techniques implemented in Octeract Engine to approach this important task.